Consensus from group interactions: An adaptive voter model on hypergraphs
Nikos Papanikolaou, Giacomo Vaccario, Erik Hormann, Renaud Lambiotte and Frank Schweitzer
Physical Review E (2022)
Projects: Network Theory
Abstract
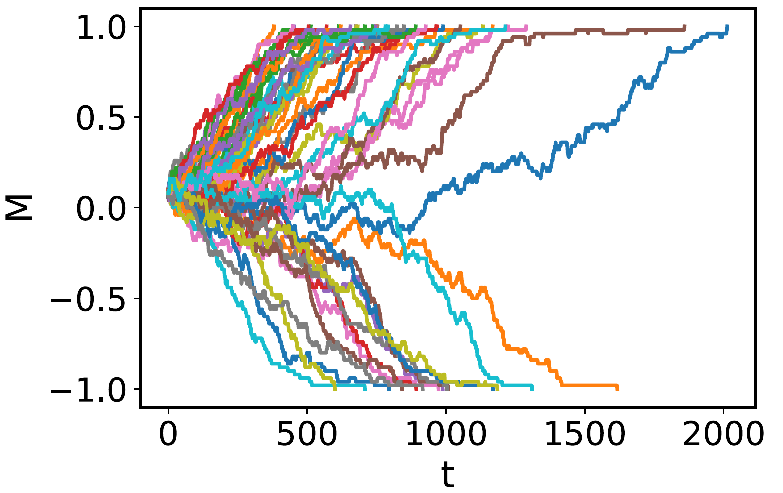
We study the effect of group interactions on the emergence of consensus in a spin system. Agents with discrete opinions (0, 1) form groups. They can change their opinion based on their group’s influence (voter dynamics), but groups can also split and merge (adaptation). In a hypergraph, these groups are represented by hyperedges of different sizes. The heterogeneity of group sizes is controlled by a parameter β. To study the impact of β on reaching consensus, we provide extensive computer simulations and compare them with an analytic approach for the dynamics of the average magnetization. We find that group interactions amplify small initial opinion biases, accelerate the formation of consensus and lead to a drift of the average magnetization. The conservation of the initial magnetization, known for basic voter models, is no longer obtained.