The optimal trajectory to control complex networks

Abstract

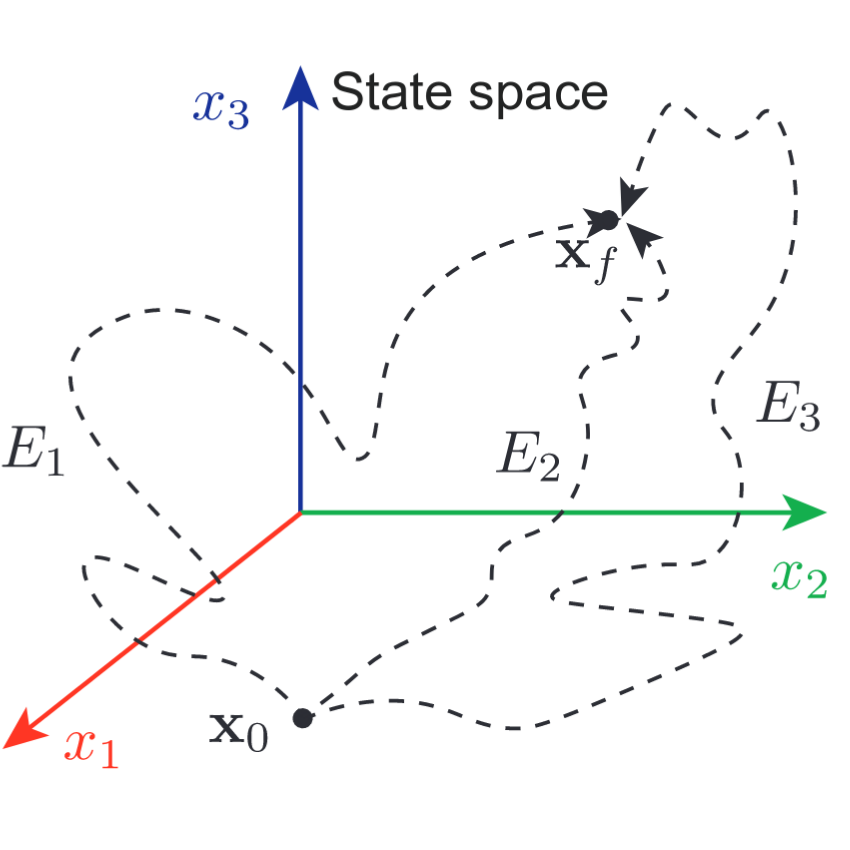
Controllability, a basic property of various networked systems, has gained profound theoretical applications in complex social, technological, biological, and brain networks. Yet, little attention has been given to the control trajectory (route), along which a controllable system can be controlled from any initial to any final state, hampering the implementation of practical control. Here we systematically uncover the fundamental relations between control trajectory and several other key factors, such as the control distance between initial and final states ($δ$), number of driver nodes, and the control time. The length ($mathcalL$) and maximum distance to the initial state ($mathcalR$) are employed to quantify the locality and globality of control trajectories. We analyze how the scaling behavior of the averaged $mathcalL$ and $mathcalR$ changes with increasing $δ$ for different initial states. After showing the scaling behavior for each trajectory, we also provide the distributions of $mathcalL$ and $mathcalR$. Further attention is given to the control time $t_f$ and its influence on $mathcalL$ and $mathcalR$. Our results provide comprehensive insights in understanding control trajectories for complex networks, and pave the way to achieve practical control in various real systems.