Bootstrapping Topological Properties and Systemic Risk of Complex Networks Using the Fitness Model
Nicolo Musmeci, Stefano Battiston, Guido Caldarelli, Michelangelo Puliga and Andrea Gabrielli
Journal of Statistical Physics (2013)
Research: Systemic Risks
Abstract
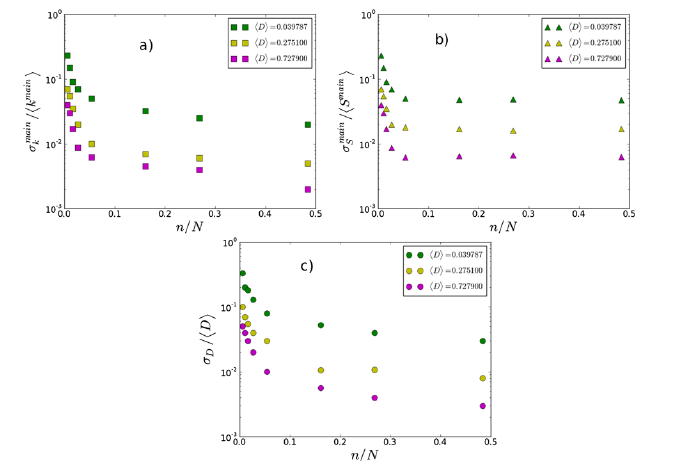
In this paper we present a novel method to reconstruct global topological properties of a complex network starting from limited information. We assume to know for all the nodes a non-topological quantity that we interpret as fitness. In contrast, we assume to know the degree, i.e. the number of connections, only for a subset of the nodes in the network. We then use a fitness model, calibrated on the subset of nodes for which degrees are known, in order to generate ensembles of networks. Here, we focus on topological properties that are relevant for processes of contagion and distress propagation in networks, i.e. network density and k-core structure, and we study how well these properties can be estimated as a function of the size of the subset of nodes utilized for the calibration. Finally, we also study how well the resilience to distress propagation in the network can be estimated using our method. We perform a first test on ensembles of synthetic networks generated with the Exponential Random Graph model, which allows to apply common tools from statistical mechanics. We then perform a second test on empirical networks taken from economic and financial contexts. In both cases, we find that a subset as small as 10 % of nodes can be enough to estimate the properties of the network along with its resilience with an error of 5 %.