Credit default swaps drawup networks: Too interconnected to be stable?

Abstract

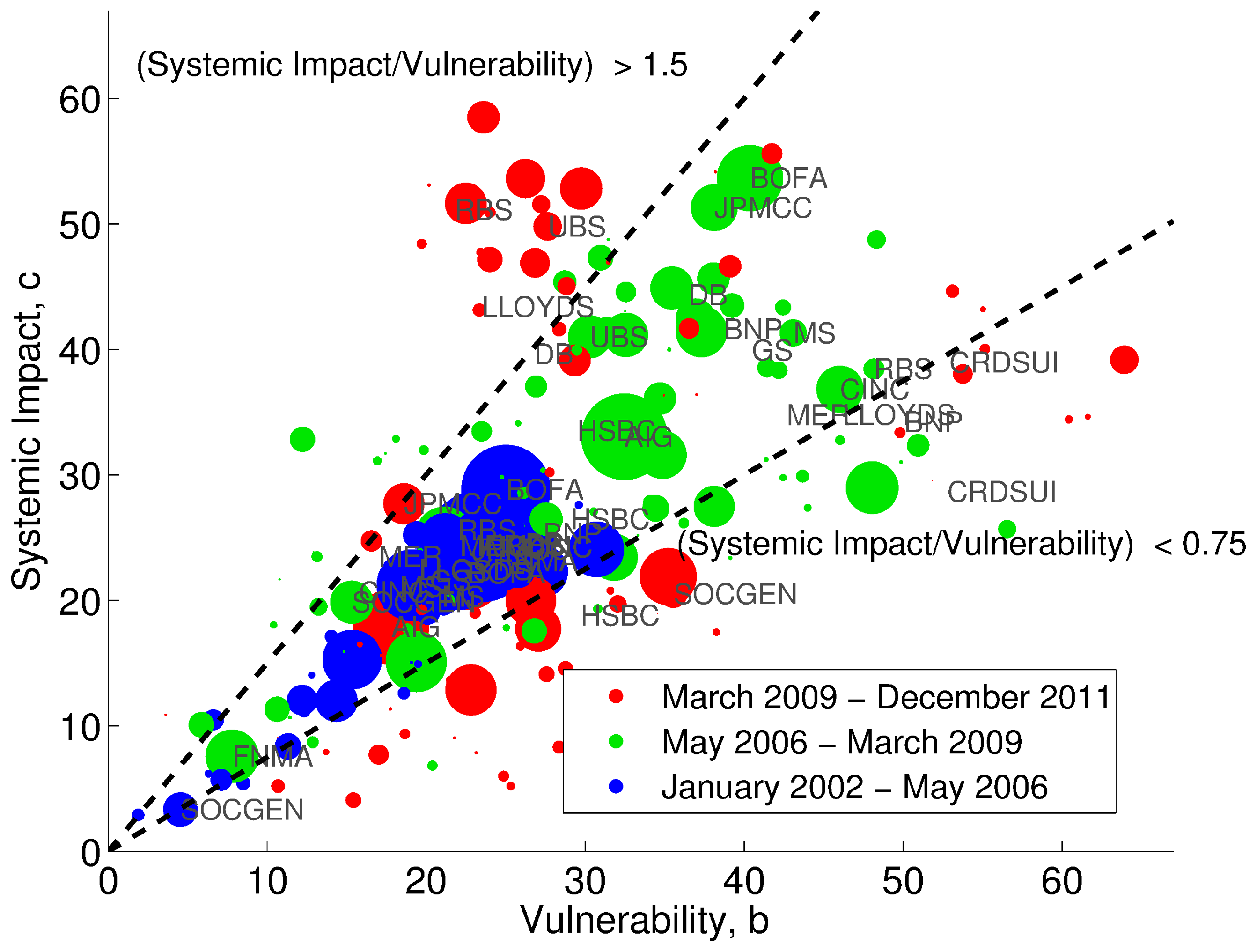
We analyse time series of CDS spreads for a set of major US and European institutions in a period overlapping the recent financial crisis. We extend the existing methodology of epsilon-drawdowns to the one of joint epsilon-drawups, in order to estimate the conditional probabilities of spike-like co-movements among pairs of spreads. After correcting for randomness and finite size effects, we find that, depending on the period of time, 50% of the pairs or more exhibit high probabilities of joint drawups and the majority of spread series are trend-reinforced, i.e. drawups tend to be followed by drawups in the same series. We then carry out a network analysis by taking the probability of joint drawups as a proxy of financial dependencies among institutions. We introduce two novel centrality-like measures that offer insights on how both the systemic impact of each node as well as its vulnerability to other nodes' shocks evolve in time.