Optimal migration promotes the outbreak of cooperation in heterogeneous populations

Abstract

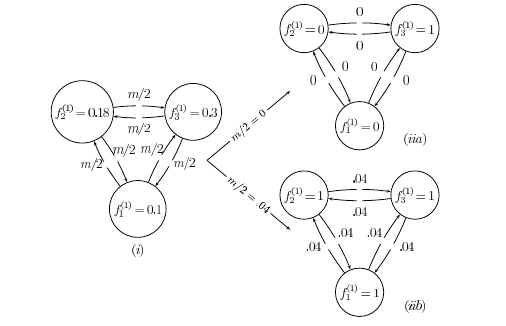
We consider a population of agents that are heterogeneous with respect to (i) their strategy when interacting ng times with other agents in an iterated prisoners dilemma game, (ii) their spatial location on K different islands. After each generation, agents adopt strategies proportional to their average payoff received. Assuming a mix of two cooperating and two defecting strategies, we first investigate for isolated islands the conditions for an exclusive domination of each of these strategies and their possible coexistence. This allows to define a threshold frequency for cooperation that, dependent on ng and the initial mix of strategies, describes the outbreak of cooperation in the absense of migration. We then allow migration of a fixed fraction of the population after each generation. Assuming a worst case scenario where all islands are occupied by defecting strategies, whereas only one island is occupied by cooperators at the threshold frequency, we determine the optimal migration rate that allows the outbreak of cooperation on all islands. We further find that the threshold frequency divided by the number of islands, i.e. the relative effort for invading defecting islands with cooperators decreases with the number of islands. We also show that there is only a small bandwidth of migration rates, to allow the outbreak of cooperation. Larger migration rates destroy cooperation.