Sustainable growth in complex networks

Abstract

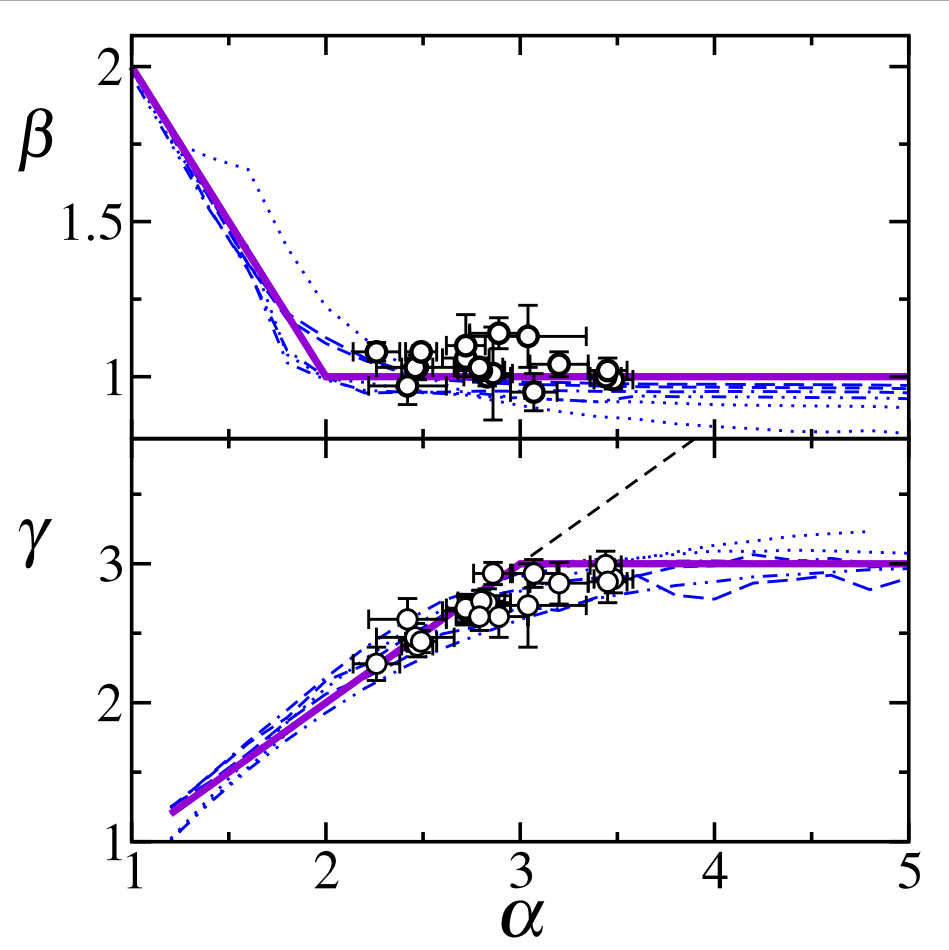
Based on the analysis of the dependency network in 18 Java projects, we develop a novel model of network growth which considers both preferential attachment and the addition of new nodes with a heterogeneous distribution of their initial degree, k0. Empirically we find that the cumulative distributions of initial and final degrees in the network follow power law behaviours: 1−P(k0)∝k1−$α$ as a function of the network size, we find empirically K(N)∝N$β$,where $β$ ∈[1.25, 2] (for small N), while converging to $β$ ∼1 for large N. This indicates a transition from a growth regime with increasing network density towards a sustainable regime, which prevents a collapse due to 0 ,and 1−P(k)∝k1−$γ$, respectively. For the total number of links ever increasing dependencies. Our theoretical framework allows us to predict relations between the exponents $α$, $β$, $γ$, which also link issues of software engineering and developer activity. These relations are verified by means of computer simulations and empirical investigations. They indicate that the growth of real Open Source Software networks occurs on the edge between two regimes, which are dominated either by the initial degree distribution of added nodes, or by the preferential attachment mechanism. Hence, the heterogeneous degree distribution of newly added nodes, found empirically, is essential to describe the laws of sustainable growth in networks.