Systemic risk in a unifying framework for cascading processes on networks
Jan Lorenz, Stefano Battiston and Frank Schweitzer
The European Physical Journal B (2009)
Research: Systemic Risks
Abstract
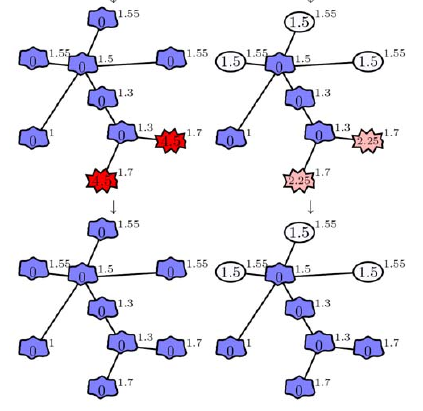
We introduce a general framework for models of cascade and contagion processes on networks, to identify their commonalities and differences. In particular, models of social and financial cascades, as well as the fiber bundle model, the voter model, and models of epidemic spreading are recovered as special cases. To unify their description, we define the net fragility of a node, which is the difference between its fragility and the threshold that determines its failure. Nodes fail if their net fragility grows above zero and their failure increases the fragility of neighbouring nodes, thus possibly triggering a cascade. In this framework, we identify three classes depending on the way the fragility of a node is increased by the failure of a neighbour. At the microscopic level, we illustrate with specific examples how the failure spreading pattern varies with the node triggering the cascade, depending on its position in the network and its degree. At the macroscopic level, systemic risk is measured as the final fraction of failed nodes, X∗,and for each of the three classes we derive a recursive equation to compute its value. The phase diagram of X∗ as a function of the initial conditions, thus allows for a prediction of the systemic risk as well as a comparison of the three different model classes. We could identify which model class leads to a first - order phase transition in systemic risk, i.e. situations where small changes in the initial conditions determine a global failure. Eventually, we generalize our framework to encompass stochastic contagion models. This indicates the potential for further generalizations.