Decelerating microdynamics can accelerate macrodynamics in the voter model

Abstract

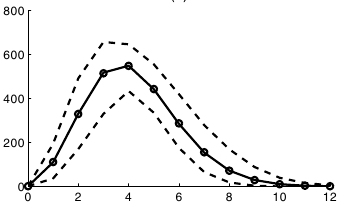
For the voter model, we study the effect of a memory-dependent transition rate. We assume that the transition of a spin into the opposite state decreases with the time it has been in its current state. Counterintuitively, we find that the time to reach a macroscopically ordered state can be accelerated by slowing down the microscopic dynamics in this way. This holds for different network topologies, including fully connected ones. We find that the ordering dynamics is governed by two competing processes which either stabilize the majority or the minority state. If the first one dominates, it accelerates the ordering of the system. The conclusions of this Letter are not restricted to the voter model, but remain valid to many other spin systems as well.