Systemic risk in a network fragility model analyzed with probability density evolution of persistent random walks
Jan Lorenz and Stefano Battiston
Networks and Heterogeneous Media (2008)
Research: Systemic Risks
Abstract
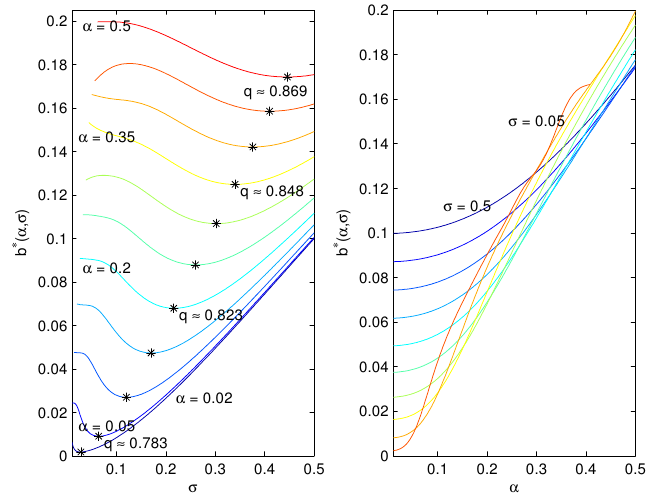
We study the mean field approximation of a recent model of cascades on networks relevant to the investigation of systemic risk control in financial networks. In the model, the hypothesis of a trend reinforcement in the stochastic process describing the fragility of the nodes, induces a trade-off in the systemic risk with respect to the density of the network. Increasing the average link density, the network is first less exposed to systemic risk, while above an intermediate value the systemic risk increases. This result offers a simple explanation for the emergence of instabilities in financial systems that get increasingly interwoven. In this paper, we study the dynamics of the probability density function of the average fragility. This converges to a unique stable distribution which can be computed numerically and can be used to estimate the systemic risk as a function of the parameters of the model.