On Algebraic Graph Theory and the Dynamics of Innovation Networks

Abstract

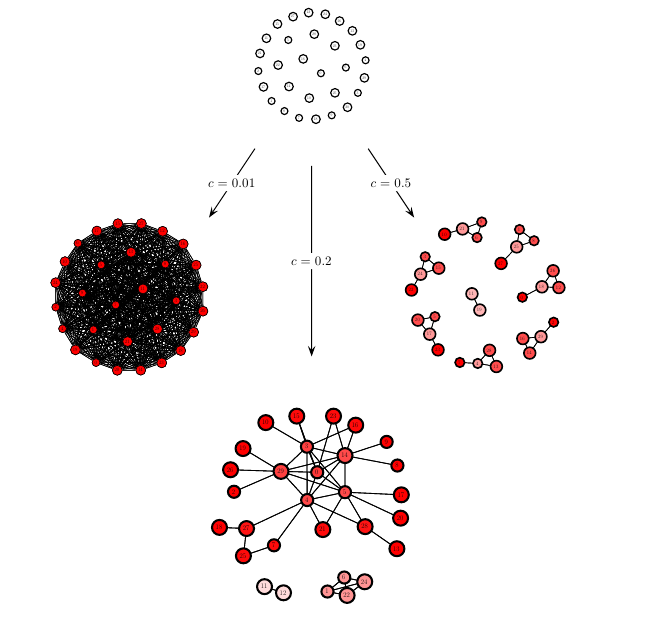
We investigate some of the properties and extensions of a dynamic innovation network model recently introduced in [Koenig et al. Games and Eco. Beh. 75-2 p694-p713 (2012)]. In the model, the set of efficient graphs ranges, depending on the cost for maintaining a link, from the complete graph to the (quasi-) star, varying within a well defined class of graphs. However, the interplay between dynamics on the nodes and topology of the network leads to equilibrium networks which are typically not efficient and are characterized, as observed in empirical studies of R&D networks, by sparseness, presence of clusters and heterogeneity of degree. In this paper, we analyze the relation between the growth rate of the knowledge stock of the agents from R&D collaborations and the properties of the adjacency matrix associated with the network of collaborations. By means of computer simulations we further investigate how the equilibrium network is affected by increasing the evaluation time $ tau$ over which agents evaluate whether to maintain a link or not. We show that only if $ tau$ is long enough, efficient networks can be obtained by the selfish link formation process of agents, otherwise the equilibrium network is inefficient. This work should assist in building a theoretical framework of R&D networks from which policies can be derived that aim at fostering efficient innovation networks.