Chaotic synchronizations of spatially extended systems as nonequilibrium phase transitions.

Abstract

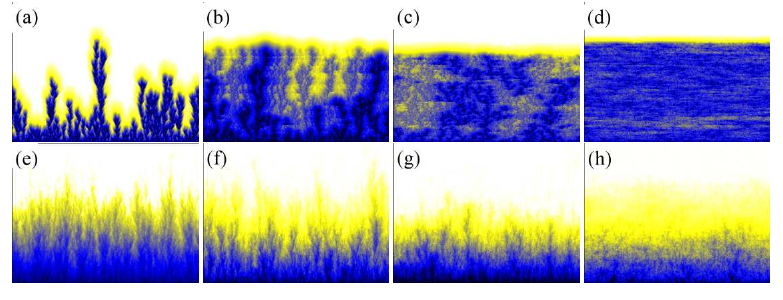
Two replicas of spatially extended chaotic systems synchronize to a common spatio-temporal chaotic state when coupled above a critical strength. As a prototype of each single spatio-temporal chaotic system a lattice of maps interacting via power-law coupling is considered. Furthermore, each unit in the one-dimensional chain is linked to the corresponding one in the replica via a local coupling. The synchronization transition is studied as a nonequilibrium phase transition, and its critical properties are analyzed at varying the spatial interaction range as well as the nonlinearity of the dynamical units composing each system. In particular, continuous and discontinuous local maps are considered. In both cases the transitions are of the second order with critical indices varying with the exponent characterizing the interaction range. For discontinuous maps it is numerically shown that the transition belongs to the anomalous directed percolation (ADP) family of universality classes, previously identified for Levy-flight spreading of epidemic processes. For continuous maps, the critical exponents are different from those characterizing ADP, but apart from the nearest-neighbor case, the identification of the corresponding universality classes remains an open problem. Finally, to test the influence of deterministic correlations for the studied synchronization transitions, the chaotic dynamical evolutions are substituted by suitable stochastic models. In this framework and for the discontinuous case, it is possible to derive an effective Langevin description that corresponds to that proposed for ADP.