Aggregate dynamics in an evolutionary network model

Abstract

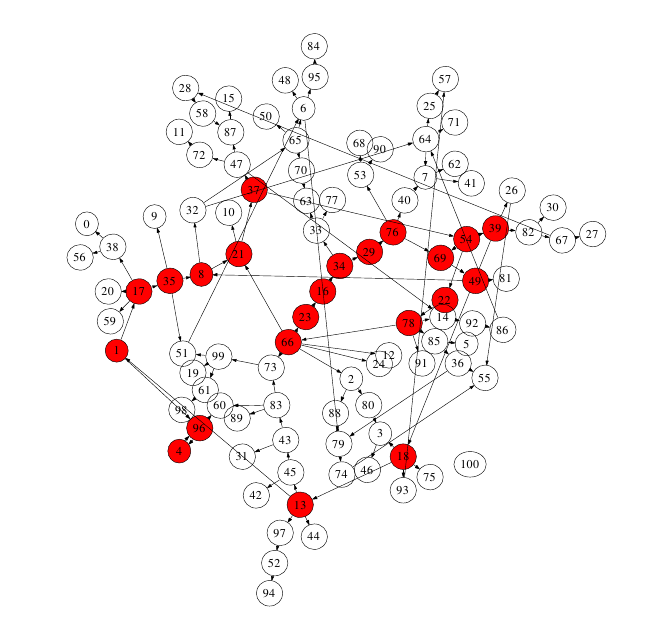
We analyze a model of interacting agents (e.g. prebiotic chemical species) which are represented by nodes of a network, whereas their interactions are mapped onto directed links between these nodes. On a fast time scale, each agent follows an eigendynamics based on catalytic support from other nodes, whereas on a much slower time scale the network evolves through selection and mutation of its nodes - agent. In the first part of the paper, we explain the dynamics of the model by means of characteristic snapshots of the network evolution and confirm earlier findings on crashes and recoveries in the network structure. In the second part, we focus on the aggregate behavior of the network dynamics. We show that the disruptions in the network structure are smoothed out, so that the average evolution can be described by a growth regime followed by a satura - tion regime, without an initial random regime. For the saturation regime, we obtain a logarithmic scaling between the average connectivity per node ls and a parameter m, describing the average incoming connectivity, which is independent of the system size N.