Continuous opinion dynamics under bounded confidence: A survey

Abstract

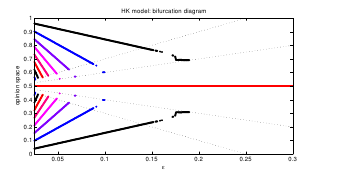
Models of continuous opinion dynamics under bounded confidence have been presented independently by Krause and Hegselmann and by Deffuant et al in 2000. They have raised a fair amount of attention in the communities of social simulation, sociophysics and complexity science. The researchers working on it come from disciplines as physics, mathematics, computer science, social psychology and philosophy. Agents hold continuous opinions which they can gradually adjust if they hear the opinions of others. The idea of bounded confidence is that agents only interact if they are close in opinion to each other. Usually, the models are analyzed with agent-based simulations in a Monte-Carlo style, but they can also be reformulated on the agent's density in the opinion space in a master-equation style. This paper is to present the agent-based and density-based modeling frameworks including the cases of multidimensional opinions and heterogeneous bounds of confidence; second, to give the bifurcation diagrams of cluster configuration in the homogeneous model with uniformly distributed initial opinions; third to review the several extensions and the evolving phenomena which have been studied so far; and fourth to state some basic open questions.