Agents with heterogeneous strategies interacting in a spatial IPD

Abstract

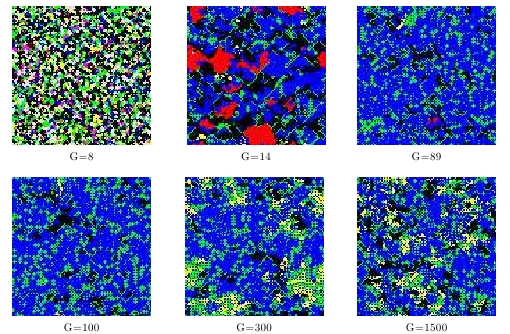
We use a spatial iterated Prisoner’s Dilemma game (IPD) to investigate the spatial - temporal evolution of heterogeneity in agents’ strategies. In our model, N agents are spatially distributed on a lattice and each agent is assumed to interact with her 4 local neighbors a number of ng times during each generation. If the agent has a one - step memory for the last action of each individual neighbor, this results in a total of eight different strategies for the game. After each generation, the agent will be replaced by an offspring that adopts the strategy of her most successful neighbor. The agents are heterogeneous in that they play different strategies dependent on (i) their past experience, (ii) their local neighborhood. The spatial - temporal distribution of these strategies is investigated by means of computer simulations on a cellular automaton. In particular, we study the incluence of ng on the dynamics of the global frequencies of the different strategies and the conditions for a stationary (frozen) or non - stationary (dynamic) coexistence of particular strategies on a spatial scale.